Article Sidebar

Download
PDF
Statistic
Read Counter : 111 Download : 29

Downloads

Download data is not yet available.

Main Article Content

Abstract

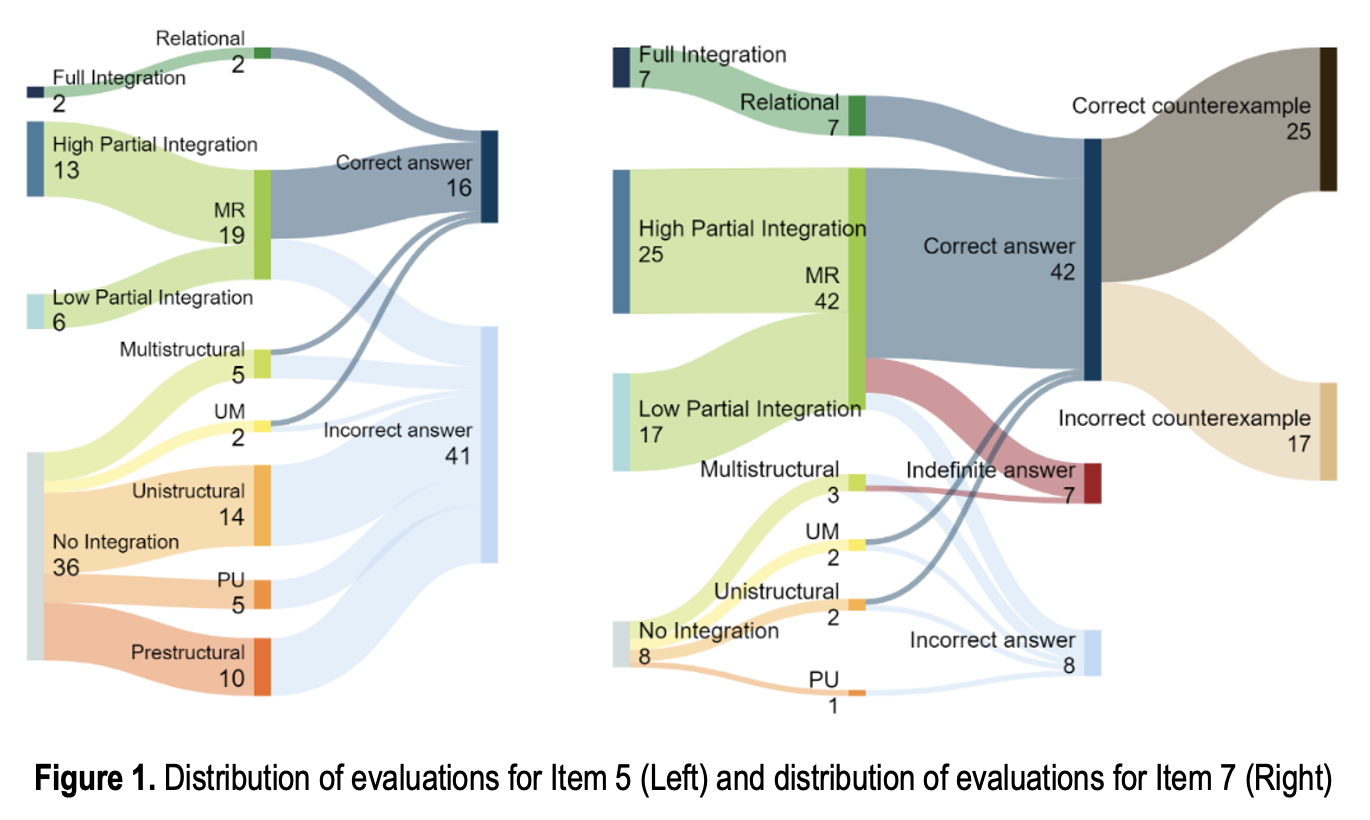
Assessing conceptual understanding in mathematics remains a persistent challenge for educators, as traditional assessment methods often prioritize procedural fluency over the complexity of connections between mathematical ideas. Consequently, these methods frequently fail to capture the depth of students’ conceptual understanding. This paper addresses this gap by developing and applying a novel rubric based on the Structure of Observed Learning Outcomes (SOLO) Taxonomy, designed to classify student responses according to demonstrated knowledge capacity and cognitive complexity. The rubric introduces transitional levels between the main SOLO categories and includes provisions for evaluating unconventional solutions, enabling a more nuanced assessment of student work based on knowledge depth and integration. The rubric was constructed through an analysis of the conceptual knowledge components required to solve each problem, validated by expert review, and guided by criteria aligned with SOLO level classifications. It also incorporates qualitative feedback to justify each SOLO level assignment. Using this rubric, the study analyzed responses from 57 first-year undergraduate students—primarily chemistry and computer science majors at a private university in the Philippines—to test items on linear approximations and the Extreme Value Theorem. Interrater reliability was established through weighted Cohen’s kappa coefficients (0.659 and 0.667 for the two items). The results demonstrate the rubric’s capacity to differentiate levels of conceptual understanding and reveal key patterns in student thinking, including reasoning gaps, reliance on symbolic manipulation, and misconceptions in mathematical logic. These findings underscore the value of the SOLO Taxonomy in evaluating complex and relational thinking and offer insights for enhancing calculus instruction. By emphasizing the interconnectedness of mathematical ideas, the study highlights the potential of conceptually oriented assessments to foster deeper learning and improve educational outcomes. Furthermore, the rubric’s adaptability suggests its applicability beyond calculus, supporting a broader shift toward concept-focused assessment practices in higher education.

Keywords

Applied Calculus Conceptual Understanding SOLO Taxonomy

Article Details

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite
Fernandez, P. J. M., & Guzon, A. F. H. (2025). A SOLO Taxonomy-based rubric for assessing conceptual understanding in applied calculus. Journal on Mathematics Education, 16(2), 559–580. https://doi.org/10.22342/jme.v16i2.pp559-580
Download Citation
Endnote/Zotero/Mendeley (RIS)
BibTeX

References

  1. Adams, D. M., McLaren, B. M., Mayer, R. E., Goguadze, G., & Isotani, S. (2013). Erroneous examples as desirable difficulty. In H. C. Lane, K. Yacef, J. Mostow, & P. Pavlik (Eds.), Artificial Intelligence in Education (pp. 803–806). Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-642-39112-5_117
  2. Alacaci, C., & Pasztor, A. (2005). On people’s incorrect either-or patterns in negating quantified statements: A study. Proceedings of the Annual Meeting of the Cognitive Science Society, 27(27), 1714-1719. https://escholarship.org/uc/item/5fz0p6m1
  3. Arslan, S. (2010). Traditional instruction of differential equations and conceptual learning. Teaching Mathematics and Its Applications, 29(2), 94–107. https://doi.org/10.1093/teamat/hrq001
  4. Bedros, V. (2003). An exploratory study of undergraduate students’ perceptions and understandings of indirect proofs. Doctoral Dissertation. The University of Montana. https://scholarworks.umt.edu/etd/9473
  5. Biggs, J., & Collis, K. (2014). Evaluating the quality of learning: The SOLO taxonomy (Structure of the observed learning outcome). Academic Press.
  6. Bisson, M.-J., Gilmore, C., Inglis, M., & Jones, I. (2016). Measuring conceptual understanding using comparative judgement. International Journal of Research in Undergraduate Mathematics Education, 2(2), 141–164. https://doi.org/10.1007/s40753-016-0024-3
  7. Bloom, B. S., Engelhart, M. D., Furst, E. J., Hill, W. H., & Krathwohl, D. R. (1964). Taxonomy of educational objectives (Vol. 2). Longmans, Green New York.
  8. Buchbinder, O., & Zaslavsky, O. (2013). Inconsistencies in students’ understanding of proof and refutation of mathematical statements. In A. M. Lindmeier & A. Heinze (Eds.), Proceedings of the 37th Conference of the International Group for the Psychology of Mathematics Education (Vol. 2, pp. 129–136). 37th Annual Conference of the International Group for the Psychology of Mathematics Education, Kiel, Germany.
  9. Büchele, S., & Feudel, F. (2023). Changes in students’ mathematical competencies at the beginning of higher education within the last decade at a German university. International Journal of Science and Mathematics Education, 21(8), 2325–2347. https://doi.org/10.1007/s10763-022-10350-x
  10. Burnett, P. C. (1999). Assessing the structure of learning outcomes from counselling using the SOLO taxonomy: An exploratory study. British Journal of Guidance & Counselling, 27(4), 567–580. https://doi.org/10.1080/03069889908256291
  11. Chan, C. C., Tsui, M. S., Chan, M. Y. C., & Hong, J. H. (2002). Applying the Structure of the Observed Learning Outcomes (SOLO) Taxonomy on student’s learning outcomes: An empirical study. Assessment & Evaluation in Higher Education, 27(6), 511–527. https://doi.org/10.1080/0260293022000020282
  12. Claudia, L. F., Kusmayadi, T. A., & Fitriana, L. (2020). The SOLO taxonomy: Classify students’ responses in solving linear program problems. Journal of Physics: Conference Series, 1538(1), 012107. https://doi.org/10.1088/1742-6596/1538/1/012107
  13. Crooks, N. M., & Alibali, M. W. (2014). Defining and measuring conceptual knowledge in mathematics. Developmental Review, 34(4), 344–377. https://doi.org/10.1016/j.dr.2014.10.001
  14. Engelbrecht, J., Bergsten, C., & Kågesten, O. (2009). Undergraduate students’ preference for procedural to conceptual solutions to mathematical problems. International Journal of Mathematical Education in Science and Technology, 40(7), 927–940. https://doi.org/10.1080/00207390903200968
  15. Ferrini-Mundy, J., & Graham, K. G. (1991). An overview of the calculus curriculum reform effort: Issues for learning, teaching, and curriculum development. The American Mathematical Monthly, 98(7), 627–635. https://doi.org/10.1080/00029890.1991.11995769
  16. Franke, M. L., Webb, N. M., Chan, A. G., Ing, M., Freund, D., & Battey, D. (2009). Teacher questioning to elicit students’ mathematical thinking in elementary school classrooms. Journal of Teacher Education, 60(4), 380–392. https://doi.org/10.1177/0022487109339906
  17. Habre, S. (2002). Writing in a reformed differential equations class. International Conference on the Teaching of Mathematics.
  18. Hicks, T., & Bostic, J. D. (2021). Formative assessment through think alouds. Mathematics Teacher: Learning and Teaching PK-12, 114(8), 598–606. https://doi.org/10.5951/MTLT.2020.0245
  19. Hillel, J. (2000). Modes of description and the problem of representation in linear algebra. In J.-L. Dorier (Ed.), On the Teaching of Linear Algebra (pp. 191–207). Springer Netherlands. https://doi.org/10.1007/0-306-47224-4_7
  20. Kågesten, O., & Engelbrecht, J. (2006). Supplementary explanations in undergraduate mathematics assessment: A forced formative writing activity. European Journal of Engineering Education, 31(6), 705–715. https://doi.org/10.1080/03043790600911803
  21. Kani, N. H. A., & Shahrill, M. (2015). Applying the thinking aloud pair problem solving strategy in mathematics lessons. Asian Journal of Management Sciences and Education, 4(2), 20–28. http://www.ajmse.leena-luna.co.jp/AJMSEPDFs/Vol.4(2)/AJMSE2015(4.2-03).pdf
  22. Kilpatrick, J., Swafford, J., & Findell, B. (Eds.). (2001). The strands of mathematical proficiency. In N. R. Council, Adding It Up: Helping Children Learn Mathematics. The National Academies Press. https://doi.org/10.17226/9822
  23. Knuth, E., Zaslavsky, O., & Ellis, A. (2019). The role and use of examples in learning to prove. The Journal of Mathematical Behavior, 53, 256–262. https://doi.org/10.1016/j.jmathb.2017.06.002
  24. Landis, J. R., & Koch, G. G. (1977). The measurement of observer agreement for categorical data. Biometrics, 33(1), 159–174. https://doi.org/10.2307/2529310
  25. Mukuka, A., Balimuttajjo, S., & Mutarutinya, V. (2020). Applying the SOLO taxonomy in assessing and fostering students’ mathematical problem-solving abilities. Problems of Education in the 21st Century, 77(6), 13.
  26. Mulbar, U., Rahman, A., & Ahmar, A. (2017). Analysis of the ability in mathematical problem-solving based on SOLO taxonomy and cognitive style. World Transactions on Engineering and Technology Education, 15(1), 68-73. http://wiete.com.au/journals/WTE&TE/Pages/Vol.15,%20No.1%20(2017)/12-Ahmar-AS.pdf
  27. Norqvist, M. (2018). The effect of explanations on mathematical reasoning tasks. International Journal of Mathematical Education in Science and Technology, 49(1), 15–30. https://doi.org/10.1080/0020739X.2017.1340679
  28. Pasani, C. F., Kusumawati, E., & Suryaningsih, Y. (2021). The ability of mathematics education students to build counterexamples in solving cyclic group problems. AIP Conference Proceedings, 2330(1), 040023. https://doi.org/10.1063/5.0043223
  29. Putri, U. H., Mardiyana, M., & Saputro, D. R. S. (2017). How to analyze the students’ thinking levels based on SOLO taxonomy? Journal of Physics: Conference Series, 895(1), 012031. https://doi.org/10.1088/1742-6596/895/1/012031
  30. Radmehr, F., & Drake, M. (2019). Revised Bloom’s taxonomy and major theories and frameworks that influence the teaching, learning, and assessment of mathematics: A comparison. International Journal of Mathematical Education in Science and Technology, 50(6), 895–920. https://doi.org/10.1080/0020739X.2018.1549336
  31. Ramos, R. A., Gutierrez, M. C., Carang, E. S. P., & Caguete, R. R. (2024). Measuring student performance in mathematics in the modern world course using bloom’s and SOLO taxonomies. International Journal of Management and Accounting, 6(3), 78–84. https://doi.org/10.34104/ijmms.024.078084
  32. Rittle-Johnson, B., & Alibali, M. W. (1999). Conceptual and procedural knowledge of mathematics: Does one lead to the other? Journal of Educational Psychology, 91(1), 175–189. https://doi.org/10.1037/0022-0663.91.1.175
  33. Santos-Trigo, M., Camacho-Machín, M., & Barrera-Mora, F. (2024). Focusing on foundational calculus ideas to understand the derivative concept via problem-solving tasks that involve the use of a dynamic geometry system. ZDM – Mathematics Education, 56(6), 1287–1301. https://doi.org/10.1007/s11858-024-01607-6
  34. Stålne, K., Kjellström, S., & Utriainen, J. (2016). Assessing complexity in learning outcomes – A comparison between the SOLO taxonomy and the model of hierarchical complexity. Assessment & Evaluation in Higher Education, 41(7), 1033–1048. https://doi.org/10.1080/02602938.2015.1047319
  35. Stipek, D. J., Givvin, K. B., Salmon, J. M., & MacGyvers, V. L. (2001). Teachers’ beliefs and practices related to mathematics instruction. Teaching and Teacher Education, 17(2), 213–226. https://doi.org/10.1016/S0742-051X(00)00052-4
  36. Stovner, R. B., Klette, K., & Nortvedt, G. A. (2021). The instructional situations in which mathematics teachers provide substantive feedback. Educational Studies in Mathematics, 108(3), 533–551. https://doi.org/10.1007/s10649-021-10065-w
  37. Sudihartinih, E. (2019). Facilitating mathematical understanding in three-dimensional geometry using the SOLO taxonomy. Erudio Journal of Educational Innovation, 6(1), 11–18. https://doi.org/10.18551/erudio.6-1.2
  38. Wilson, M. (2009). Measuring progressions: Assessment structures underlying a learning progression. Journal of Research in Science Teaching, 46(6), 716–730. https://doi.org/10.1002/tea.20318