Article Sidebar

Download
PDF
Statistic
Read Counter : 147 Download : 68

Downloads

Download data is not yet available.

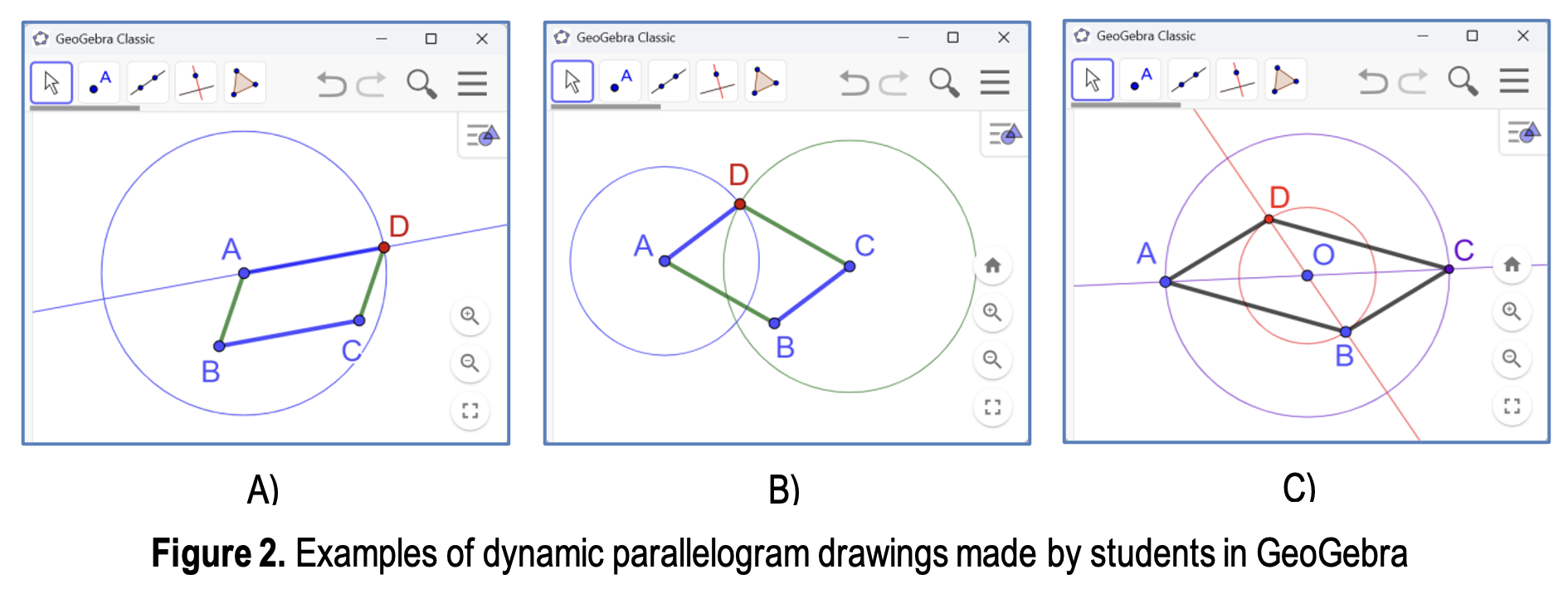
Main Article Content

Abstract

Research in mathematics education has increasingly emphasized the importance of developing deep conceptual understanding and higher-order thinking skills in geometry learning. However, traditional approaches to teaching elementary geometry in teacher education programs often remain procedural and insufficiently foster progression through the Van Hiele levels of geometric thinking. Addressing this gap, the present study introduces and examines the method of local axiomatization as a novel instructional approach for preparing future mathematics teachers. The purpose of the study is to identify, characterize, and test practical strategies for teaching an "Elementary Geometry" course through this method, with the goal of facilitating teacher candidates’ advancement across the Van Hiele model of geometric thinking. The research highlights effective educational practices, including maintaining student motivation, inquiry-based learning, collaborative interaction, integration of technology, strategic problem-solving, and reflective error analysis. Based on these principles, a university-level course in elementary geometry was designed and implemented as research training for 56 prospective mathematics teachers. Data were collected through the Van Hiele Geometry Test (VHGT), administered before and after the intervention, and through reflective essays written by participants. Statistical analysis using the Pearson criterion demonstrated a significant increase in students’ levels of geometric thinking, while qualitative reflections indicated enrichment of geometric knowledge and more independent, yet guided, learning. The findings suggest that the method of local axiomatization, despite implementation challenges, can serve as an effective and innovative pedagogical framework in mathematics teacher education, contributing to the development of both conceptual understanding and reflective practice in geometry learning.

Keywords

Elementary Geometry Future Mathematics Teachers Geometric Teacher Training Geometric Thinking Local Axiomatization Teacher Education Van Hiele Model

Article Details

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite
Shmigirilova, I. B., Rvanova, A. S., Tadzhigitov, A. A., & Beloshistova, Y. S. (2025). Advancing future mathematics teachers’ geometric thinking through a Van Hiele-based elementary geometry course. Journal on Mathematics Education, 16(3), 799–818. https://doi.org/10.22342/jme.v16i3.pp799-818
Download Citation
Endnote/Zotero/Mendeley (RIS)
BibTeX

References

  1. Al-ebous, T. (2016). Effect of the Van Hiele model in geometric concepts acquisition: The attitudes towards geometry and learning transfer effect of the first three grades students in Jordan. International Education Studies, 9(4), 87. https://doi.org/10.5539/ies.v9n4p87
  2. Alex, J. K., & Mammen, K. J. (2016). Lessons learnt from employing Van Hiele theory based instruction in senior secondary school geometry classrooms. Eurasia Journal of Mathematics, Science & Technology Education, 12(8), 2223–2236. https://10.12973/eurasia.2016.1228a
  3. Altakhyneh, B. H. (2018). Levels of geometrical thinking of students receiving blended learning in Jordan. Journal of Education and Learning, 12(2), 159–165 https://doi.org/10.11591/edulearn.v12i2.8289
  4. Armah, R. B., Cofie, P. O., & Okpoti, Ch. A. (2017). The geometric thinking levels of pre-service teachers in Ghana. Higher Education Research, 2(3), 98–106. https://doi.org/10.11648/j.her.20170203.14
  5. Armah, R. B., & Kissi, P. S. (2019). Use of the Van hiele theory in investigating teaching strategies used by college of education geometry tutors. EURASIA Journal of Mathematics, Science and Technology Education, 15(4), em1694. https://doi.org/10.29333/ejmste/103562
  6. Awi, A., Naufal, M. A., Sutamrin, S., & Huda, M. (2024). Enhancing geometry achievement in pre-service mathematics teachers: The impact of a scaffolded flipped classroom using a learning management system. Journal of Ecohumanism, 3(6), 637–645. https://doi.org/10.62754/joe.v3i6.4035
  7. Bernard, M., & Setiawan, W. (2020). Development of geometry analysis using GeoGebra scripting in terms of student cognitive capabilities. Journal of Physics: Conference Series, 1521(3), 032103. https://doi.org/10.1088/1742-6596/1521/3/032103
  8. Bonyah, E., & Larbi, E. (2021). Assessing Van Hiele’s geometric thinking levels among elementary pre-service mathematics teachers. African Educational Research Journal, 9(4), 844–851. https://doi.org/10.30918/AERJ.94.21.119
  9. Chen, W.-W. (2015). The relations between perceived parenting styles and academic achievement in Hong Kong: The mediating role of students' goal orientations. Learning and Individual Differences, 37, 48–54. https://doi.org/10.1016/j.lindif.2014.11.021
  10. Chen, Y.-H., Senk, S.L., Thompson, D.R., Voogt, K. (2019). Examining psychometric properties and level classification of the Van Hiele geometry test using CTT and CDM frameworks. Journal of Educational Measurement, 56, 733–756. https://doi.org/10.1111/jedm.12235
  11. Clark-Wilson, A., Robutti, O., & Thomas, M. (2020). Teaching with digital technology. ZDM –Mathematics Education, 52, 1223–1242. https://doi.org/10.1007/s11858-020-01196-0
  12. Code, W., Merchant, S., Maciejewski, W., Thomas, M., & Lo, J. (2016). The mathematics attitudes and perceptions survey: An instrument to assess expert-like views and dispositions among undergraduate mathematics students. International Journal of Mathematical Education in Science and Technology, 47(6), 917–937. https://doi.org/10.1080/0020739X.2015.1133854
  13. Dalinger, V. A. (2015). Keis-metod v obuchenii budushchikh uchitelei matematiki kursu "Tipichnye oshibki, ikh prichiny i puti preduprezhdeniia" [Case method in teaching future mathematics teachers the course "Typical mistakes, their causes and ways of prevention"]. Mezhdunarodnyi zhurnal eksperimental'nogo obrazovaniia, 3(4), 571–573. from https://expeducation.ru/ru/article/view?id=7339 (In Russ.)
  14. Fathurrohman, M., Porter, A. L., & Worthy, A. L. (2017). Teachers’ real and perceived of ICT supported-situation for mathematics teaching and learning. International Journal on Emerging Mathematics Education, 1(1), 11–24. http://dx.doi.org/10.12928/ijeme.v1i1.5695
  15. Fitriyani, H., Widodo, S. A., & Hendroanto, A. (2018). Students’ geometric thinking based on van Hiele’s theory. Infinity Journal, 7(1), 55–60. https://doi.org/10.22460/infinity.v7i1.p53-60
  16. Freudenthal, H. (1973). Mathematics as an educational task. D. Reidel, Dordrecht, Holland. https://doi.org/10.1007/978-94-010-2903-2
  17. Fridman, L. M. (2005). Teoreticheskie osnovy metodiki obucheniia matematike [Theoretical foundations of methods of teaching mathematics]. Moskva. (In Russ.)
  18. Fried, M. N. (2014). Mathematics & mathematics education: Searching for common ground. In M.N. Fried, T. Dreyfus (Eds.), Mathematics & Mathematics Education: Searching for 3 Common Ground, Advances in Mathematics Education. (p. 3–22). Springer https://doi.org/10.1007/978-94-007-7473-5_1
  19. García-Lázaro, D., & Martín-Nieto, R. (2023). Mathematical and digital competence of future teachers using GeoGebra application. Alteridad, 18(1), 83–96. https://doi.org/10.17163/alt.v18n1.2023.07
  20. Guberman, R., & Leikin R. (2013). Interesting and difficult mathematical problems: Changing teachers’ views by employing multiple-solution tasks. Journal of Mathematics Teacher Education, 16(1), 33‒56. https://doi.org/10.1007/s10857-012-9210-7
  21. Halat, E., & Şahin, O. (2008). Van Hiele levels of pre- and in-service Turkish elementary school teachers and gender related differences in geometry. The Mathematics Educator, 11(1/2), 143‒158.
  22. Hassan, M. N., Abdullah, A. H., & Ismail, N. (2020). Effects of integrative interventions with Van Hiele phase on students’ geometric thinking: A systematic review. Journal of Critical Reviews, 7(13), 1133–1140. https://doi.org/10.31838/jcr.07.13.194
  23. Hemker, L., Prescher, C., & Narciss, S. (2017). Design and evaluation of a problem-based learning environment for teacher training. Interdisciplinary Journal of Problem-Based Learning, 11(2), 10, https://doi.org/10.7771/1541-5015.1676
  24. Hillmayr, D., Ziernwald, L., Reinhold, F., Hofer, S. I., & Reiss, K. M. (2020). The potential of digital tools to enhance mathematics and science learning in secondary schools: A context-specific meta-analysis. Computers & Education, 153, 103897. https://doi.org/10.1016/j.compedu.2020.103897
  25. Hourigan, M., & Leavy, A. M. (2017). Preservice primary teachers’ geometric thinking: Is pre-tertiary mathematics education building sufficiently strong foundations? The Teacher Educator, 52(4), 346-364. https://doi.org/10.1080/08878730.2017.1349226
  26. Howe, C., Hennessy, S., Mercer, N., Vrikki, M., & Wheatley, L. (2019). Teacher–student dialogue during classroom teaching: Does it really impact on student outcomes? The Journal of the Learning Sciences, 28(4–5), 462–512. https://doi.org/10.1080/10508406.2019.1573730
  27. Karakuş, F., & Peker, M. (2015). The effects of dynamic geometry software and physical manipulatives on pre-service primary teachers’ Van Hiele levels and spatial abilities. Turkish Journal of Computer and Mathematics Education (TURCOMAT), 6(3), 338–365. https://doi.org/10.16949/turcomat.31338
  28. Klemer, A., & Rapoport, S. (2020). Origami and GeoGebra activities contribute to geometric thinking in second graders. Eurasia Journal of Mathematics, Science and Technology Education, 16(11), 3–12. https://doi.org/10.29333/ejmste/8537
  29. Koyunlu, U. Z., & Dokme, I. (2020). The effect of technology-supported inquiry-based learning in science education: Action research. Journal of Education in Science, Environment and Health (JESEH), 6(2), 120–133. http://doi.org/10.21891/jeseh.632375
  30. Krygowska, A. Z. (1971). Treatment of the Axiomatic Method in Class. In Servais, W. & Varga, T., Teaching School Mathematics, Penguin-Unesco, London (124–150)
  31. Kutluca, T. (2013). The effect of geometry instruction with dynamic geometry software; GeoGebra on van Hiele geometry understanding levels of students. Educational Research and Reviews, 8(17), 1509–1518. https://doi.org/10.5897/ERR2013.1554
  32. Kuzniak, A. (2008). Personal Geometrical Working Space: a Didactic and Statistical Approach. In: Gras, R., Suzuki, E., Guillet, F., Spagnolo, F. (eds) Statistical Implicative Analysis. Studies in Computational Intelligence, 27. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-78983-3_9
  33. Küçük, K., & Gün, Ö. (2023). The effects of GeoGebra-assisted transformation geometry instruction on student achievement, attitudes, and beliefs. Journal of Computer and Education Research, 11(22), 671–690. https://doi.org/10.18009/jcer.1324668
  34. Lynch, D.J., & Trujillo, H. (2011). Motivational beliefs and learning strategies in organic chemistry. International Journal of Science and Mathematics Education, 9, 1351–1365 https://doi.org/10.1007/s10763-010-9264-x
  35. Mallue, T. (2018). What is error analysis, and how can it be used in a mathematics classroom? Learning to Teach Language Arts, Mathematics, Science, and Social Studies Through Research and Practice, 7(1), 54-58. https://openjournals.utoledo.edu/index.php/learningtoteach/article/view/259/138
  36. Marrades, R., & Gutiérrez, A. (2025). The van Hiele model, students’ proofs, and dynamic geometry: A review of research. ZDM – Mathematics Education, 57(2), 233–250. https://doi.org/10.1007/s11858-025-01703-1
  37. Matos, L., Lens, W., Vansteenkiste, M., & Mouratidis, A. (2017). Optimal motivation in Peruvian high schools: Should learners pursue and teachers promote mastery goals, performance-approach goals or both? Learning & Individual Differences, 55, 87–96. https://doi.org/10.1016/j.lindif.2017.02.003
  38. Meilinda, M., Indra Putri, R., Zulkardi, Z., Inderawati, R., & Desnita, T. (2024). Enhancing teacher competence through collaborative worksheet development: An empirical investigation. International Journal of Evaluation and Research in Education (IJERE), 13(3). 1690-1702. https://doi.org/10.11591/ijere.v13i3.27266
  39. Milner, A., & Scholkmann, A. (2023). Future teachers for future societies: Transforming teacher professionalism through problem-based professional learning and development. Professional Development in Education, 49(4), 739-751. https://doi.org/10.1080/19415257.2023.2203173
  40. Moreno, M., Llinares, S., & Santonja, P. (2024). Prospective secondary mathematics teachers’ use of inquiry-based teaching principles as conceptual tools when modifying mathematical tasks. Journal on Mathematics Education, 15(4), 1131–1152. https://doi.org/10.22342/jme.v15i4.pp1131-1152
  41. Ni, Y., Zhou, D.-H. R., Cai, J., Li, X., Li, Q., & Sun, I. X. (2018). Improving cognitive and affective learning outcomes of students through mathematics instructional tasks of high cognitive demand. Journal of Educational Research, 111(6), 704–719. https://doi.org/10.1080/00220671.2017.1402748
  42. Niroj, D., Binod, P., Mani, S. I., & Netra, M. (2022). Use of GeoGebra in Teaching and Learning Geometric Transformation in School Mathematics. International Journal of Interactive Mobile Technologies (iJIM), 16(8), 65–78, https://doi.org/10.3991/ijim.v16i08.29575
  43. Ramlan, A. M., & Hali, F. (2018). Analysis of the difficulty of mathematical education students in completing the geometric running problem based on van Hiele theory in geometry transformation. Journal of Mathematics Education, 3(2), 65–70. http://doi.org/10.31327/jomedu.v3i2.834
  44. Roldán-Zafra, J., Perea, C., Polo-Blanco, I. & Campillo, P. (2022). Design of an interactive module based on the van Hiele model: Case study of the Pythagorean theorem. International Electronic Journal of Mathematics Education, 17(1), em0672. https://doi.org/10.29333/iejme/11556
  45. Rvanova, A. S. (2018). Dinamicheskie modeli v obuchenii geometrii v kontekste razvitiia kriticheskogo myshleniia [Dynamic models in teaching geometry in the context of developing critical thinking]. Vestnik Severo-Kazakhstanskogo Universiteta imeni M. Kozybaeva, (1(38)), 51–56. https://vestnik.ku.edu.kz/jour/article/view/404/408 (In Russ.)
  46. Santos, M. S., Medida D, Monaliza L. S., & Arlene D. H. (2022). The Van Hiele model in teaching geometry. World Journal of Vocational Education and Training, 4(1), 10–22. https://doi.org/10.18488/119.v4i1.3087
  47. Santos-Trigo, M. (2024). Problem solving in mathematics education: Tracing its foundations and current research-practice trends. ZDM – Mathematics Education, 56(2), 211-222. https://doi.org/10.1007/s11858-024-01578-8
  48. Shaughnessy, M., DeFino, R., Pfaff, E., & Blunk, M. (2021). I think I made a mistake: How do prospective teachers elicit the thinking of a student who has made a mistake? Journal of Mathematics Teacher Education, 24(4), 335–359. https://doi.org/10.1007/s10857-020-09461-5
  49. Shkerina, L. V., Shashkina, M. B., & Tabinova, O. A. (2022). Vyiavlenie i preodolenie predmetnykh defitsitov studentov – budushchikh uchitelei matematiki [Identification and overcoming of subject-related deficits in students — future mathematics teachers]. Perspektivy nauki i obrazovania – Perspectives of Science and Education, 58(4), 173–192. https://doi.org/10.32744/pse.2022.4.11(In Russ.)
  50. Shmigirilova, I. B., Chugunova, A. A., & Pustovalova, N. I. (2019). Razvitie analitiko-sinteticheskoi deiatel'nosti studentov v protsesse obucheniia matematicheskomu analizu [Development of analytical and synthetic activity of students in the process of learning mathematical analysis]. Science for Education Today, 9(3), 121–137. http://dx.doi.org/10.15293/2658-6762.1903.07 (In Russ.)
  51. Smith, J. M., & Mancy, R. (2018). Exploring the relationship between metacognitive and collaborative talk during group mathematical problem-solving – What do we mean by collaborative metacognition? Research in Mathematics Education, 20(1), 14–36. https://doi.org/10.1080/14794802.2017
  52. Stoliar, A. A. (1974). Pedagogika matematiki [Pedagogy of mathematics]. Minsk: Vysshaia shkola. (In Russ.)
  53. Sudihartinih, E., & Wahyudin. (2019). The Van Hiele levels of geometric of students in first semester reviewed from gender. Journal of Physics: Conference Series, 1280(4), 042034. https://doi.org/10.1088/1742-6596/1280/4/042034
  54. Sunzuma, G. (2023). Technology integration in geometry teaching and learning: A systematic review (2010–2022). LUMAT, 11(3), 1–18. https://doi.org/10.31129/LUMAT.11.3.1938
  55. Taggart, J. & Wheeler, L. B. (2023). Collaborative learning as constructivist practice: An exploratory qualitative descriptive study of faculty approaches to student group work. Active Learning in Higher Education, 26(1), 59-76. https://doi.org/10.1177/14697874231193938
  56. Tall, D. (2019). Making sense of mathematical thinking over the long term: The framework of three worlds of mathematics and new developments. Available online: https://homepages.warwick.ac.uk/staff/David.Tall/pdfs/dot2020a-3worlds-extension.pdf
  57. Thurm, D., & Barzel, B. (2020). Effects of a professional development program for teaching mathematics with technology on teachers’ beliefs, self-efficacy and practices. ZDM – Mathematics Education, 52, 1411–1422. https://doi.org/10.1007/s11858-020-01158-6
  58. Thurlings, M., & den Brok, P. (2018). Student teachers’ and in-service teachers’ peer learning: A realist synthesis. Educational Research and Evaluation, 24(1-2), 13–50.
  59. Usiskin, Z. (1982). Van Hiele Levels and achievement in secondary school geometry: Cognitive development and achievement in secondary school geometry project. University of Chicago Press.
  60. Usman, H., Yew, W. T., & Saleh, S. (2020). Effects of van Hiele’s phase-based teaching strategy and gender on pre-service mathematics teachers’ geometry achievement in Niger State, Nigeria. International Journal of Pedagogical Development and Lifelong Learning, 1(1), 1-8. https://doi.org/10.30935/ijpdll/8363
  61. Van Hiele, P. M. (1984). A Child’s Thought and Geometry. In English Translation of Selected Writings of Dina Van Hiele-Geldof and Pierre M. Van Hiele. D. Fuys, D. Geddes, R. W. Tischler (Eds). Brooklyn.
  62. Vishnumolakala, V. R., Southam, D. C., Treagust, D. F., Mocerino, M., & Qureshi, S. (2017). Students’ attitudes, self-efficacy and experiences in a modified process-oriented guided inquiry learning undergraduate chemistry classroom. Chemistry Education Research and Practice, 18(2), 340–352. https://doi.org/10.1039/c6rp00233a
  63. Žilková, K., Záhorec, J., & Munk, M. (2025). Analysis of the level of geometric thinking of pupils in Slovakia. Education Sciences, 15(8), 1020. https://doi.org/10.3390/educsci15081020