Article Sidebar

Download
PDF
Statistic
Read Counter : 0 Download : 0

Downloads

Download data is not yet available.

Main Article Content

Abstract

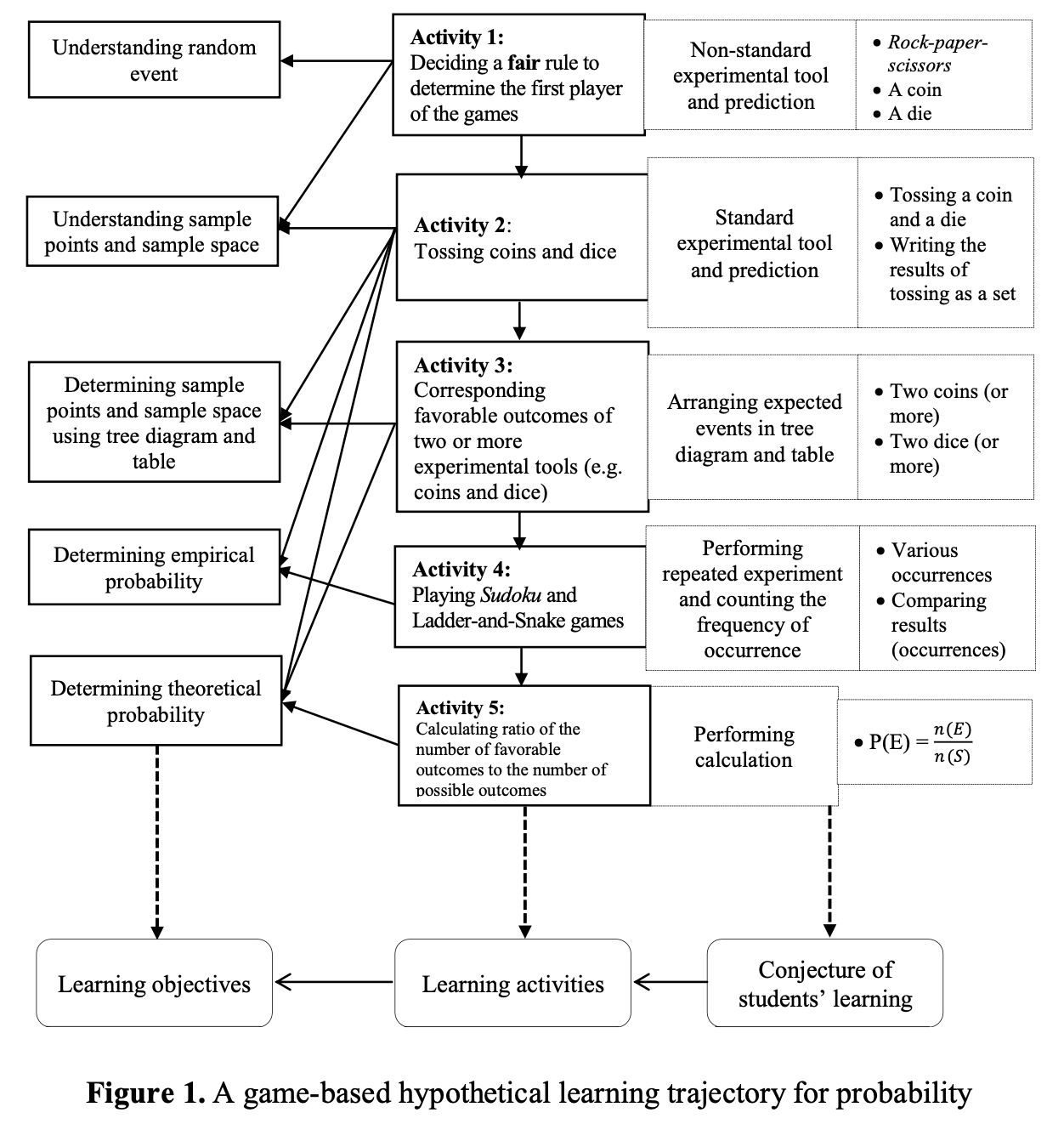
This research is aimed to describe a learning trajectory for probability through game-based learning. The research employed design research consisting of three stages: preparing for the experiment, design experiment, and retrospective analysis. A hypothetical learning trajectory (HLT) using Sudoku and Snake-and-ladder games was developed by collecting data through documentation, interviews, and classroom observations. The HLT was implemented in the classroom to investigate students’ actual learning trajectory. The results of this research indicate that the games helped students understand the concept of probability. The learning trajectory for probability based on game-based learning is seen from the perspective of four levels of emergent modeling. In the first level – ‘situational level’ – Sudoku and Ladder-and-Snake games were played by students. The second level is the ‘referential level’ where the rules of the games were used as a starting point to learn the concept of probability. Communication during game playing stimulated students' knowledge about random events, sample spaces, sample points, and events. At the third level – ‘general level’ – students used tree and table diagrams to generalize possible outcomes of an experiment and develop an understanding of sample spaces and sample points. Lastly, at the ‘formal level’ students developed their informal knowledge into formal concepts of probabilities.

Keywords

design research four levels of modelling game-based learning learning trajectory probability

Article Details

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite
Wijaya, A., Elmaini, & Doorman, M. (2021). A learning trajectory for probability: A case of game-based learning. Journal on Mathematics Education, 12(1), 1–16. Retrieved from http://jme.ejournal.unsri.ac.id/index.php/jme/article/view/3673
Download Citation
Endnote/Zotero/Mendeley (RIS)
BibTeX

References

  1. Amador, J., & Lamberg, T. (2013). Learning trajectories, lesson planning, affordances, and constraints in the design and enactment of mathematic teaching. Mathematical Thinking and Learning, 15(2), 146-170. https://doi.org/10.1080/10986065.2013.770719
  2. Bryant, P., & Nunes, T. (2012). Children’s understanding of probability A literature review (summary report). London: Nuffield Foundation.
  3. Clements, D. H., Wilson, D. C., & Sarama, J. (2004). Young Children's Composition of Geometric Figures: A Learning Trajectory. Mathematical Thinking and Learning, 6(2), 163-184. http://dx.doi.org/10.1207/s15327833mtl0602_5
  4. Clements, D. H., & Sarama, J. (2009). Learning and teaching early math: The learning trajectories approach. New York: Routledge.
  5. Daro, P., Mosher, F. A., & Corcoran, T. (2011). Learning trajectories in mathematics. A foundation for standards, curriculum, assessment, and instruction. Philadelphia: Consortium for Policy Research in Education.
  6. de Beer, H., Gravemeijer, K., & van Eijck, M. (2017). A proposed local instruction theory for teaching instantaneous speed in grade five. The Mathematics Enthusiast, 14(1), 435-468. Available at: https://scholarworks.umt.edu/tme/vol14/iss1/24
  7. Doorman, L. M., & Gravemeijer, K. P. E. (2009). Emergent modelling: Discrete graphs to support the understanding of change and velocity. ZDM: International Journal on Mathematics Education, 41(1), 199-211. https://doi.org/10.1007/s11858-008-0130-z
  8. Fischbein, E. (2002). Intuition in science and mathematics: An educational approach. Doordrecht: Springer.
  9. Frykholm, J. A. (2001). Building on intuitive notions of chance. Teaching Children Mathematics, 8(2), 112-117.
  10. Gravemeijer, K. (1994). Developing realistic mathematics education. Utrecht: Freudenthal Institute.
  11. Gravemeijer, K., Bowers, J., & Stephan, M. (2003). A hypothetical learning trajectory on measurement and flexible arithmetic. In M. Stephan, J. Bowers, P. Cobb & K. Gravemeijer (Eds.), Supporting students’ development of measuring conceptions: Analyzing students’ learning in social context (pp. 51-66). JRME Monograph 12. Reston, VA: National Council of Teacher of Mathematics.
  12. Gravemeijer, K. & Cobb, P. (2013). Design research from a learning design perspective. In T. Plomp & N. Nieveen (Eds.), Educational design research (pp. 17-51). London: Routledge.
  13. Jun, L. (2000). Chinese students’ understanding of probability. Unpublished Doctoral Dissertation. Singapore: National Institute of Education, Nanyang Technological University.
  14. Kennedy, L. M., Tipps, S., & Johnson, A. (2008). Guiding children’s learning of mathematics. Belmont: Thomson Higher Education.
  15. Lobato, J., & Walters, C. D. (2017). A taxonomy of approaches to learning trajectories and progressions. In J. Cai (Ed.), Compendium for research in mathematics education (pp. 74-101). Reston, VA: National Council of Teacher of Mathematics.
  16. Mayer, R. E. (2002). Rote versus meaningful learning. Theory into practice, 41(4), 226-232. https://doi.org/10.1207/s15430421tip4104_4
  17. Mojica, G. F., & Confrey, J. (2009). Pre-service elementary teachers’ understanding of an equipartitioning learning trajectory. Proceeding of the 31st annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education. Atlanta: George State University.
  18. Nickerson, S. D. & Whitacre, I. (2010). A local instruction theory for the development of number sense. Mathematical Thinking and Learning, 12(3), 227-252. https://doi.org/10.1080/10986061003689618
  19. OECD. (2009). PISA 2009 Assessment Framework - Key Competencies in Reading, Mathematics and Science. Paris: OECD.
  20. OECD. (2016). PISA 2015 Assessment and Analytical Framework: Science, Reading, Mathematic and Financial Literacy. Paris: OECD Publishing.
  21. Paparistodemou, E., Noss, R., & Pratt, D. (2008). The interplay between fairness and randomness in a spatial computer game. International Journal of Computers for Mathematical Learning, 13(2), 89-110. https://doi.org/10.1007/s10758-008-9132-8
  22. Perry, B. & Dockett, S. (2002). Young children’s access to powerful mathematical ideas. In L. D. English (Ed.), Handbook of international research in mathematics education (pp. 81-112). Mahwah, New Jersey: Lawrence Erlbaum Associates, Inc.
  23. Risdiyanti, I., & Prahmana, R.C.I. (2020). The learning trajectory of number pattern learning using Barathayudha war stories and Uno Stacko. Journal on Mathematics Education, 11(1), 157-166. http://doi.org/10.22342/jme.11.1.10225.157-166
  24. Schneider, M. C., & Gowan, P. (2013). Investigating teachers’ skills in interpreting evidence of student learning. Applied Measurement in Education, 26(3), 191-204. https://doi.org/10.1080/08957347.2013.793185
  25. Shanty, N. O. (2016). Investigating students’ development of learning integer concept and integer addition. Journal on Mathematics Education, 7(2), 57-72. https://doi.org/10.22342/jme.7.2.3538.57-72
  26. Simon, M. A. (1995). Reconstructing mathematics pedagogy from a constructivist perspective. Journal for Research in Mathematics Education, 26(2), 114-145. https://doi.org/10.5951/jresematheduc.26.2.0114
  27. Simon, M. A. & Tzur, R. (2004). Explicating the Role of Mathematical Tasks in Conceptual Learning: An Elaboration of the Hypothetical Learning Trajectory. Mathematical Thinking and Learning, 6(2), 91-104. http://dx.doi.org/10.1207/s15327833mtl0602_2
  28. Smith, G. (1998). Introduction to statistical reasoning. New York: McGraw-Hill Science, Engineering & Mathematics.
  29. Steffe, L. P. (2004) On the construction of learning trajectories of children: The case of commensurate fractions. Mathematical Thinking and Learning, 6(2), 129-162. http://dx.doi.org/10.1207/s15327833mtl0602_4
  30. Sztajn, P., Confrey, J., Wilson, P. H., & Edgington, C. (2012). Learning trajectory based instruction: Toward a theory of teaching. Educational Researcher, 41(5), 147-156. https://doi.org/10.3102/0013189x12442801
  31. Wijaya, A., Doorman, M. L., & Keijzer, R. (2011). Emergent modelling: From traditional Indonesian games to a standard unit of measurement. Journal of Science and Mathematics Education in Southeast Asia, 34(2), 149-173.
  32. Wilson, P. H., Sztajn, P., Edgington, C., & Myers, M. (2015). Teachers’ uses of a learning trajectory in student-centered instructional practices. Journal of Teacher Education, 66(3), 227-244. https://doi.org/10.1177/0022487115574104