Main Article Content
Abstract
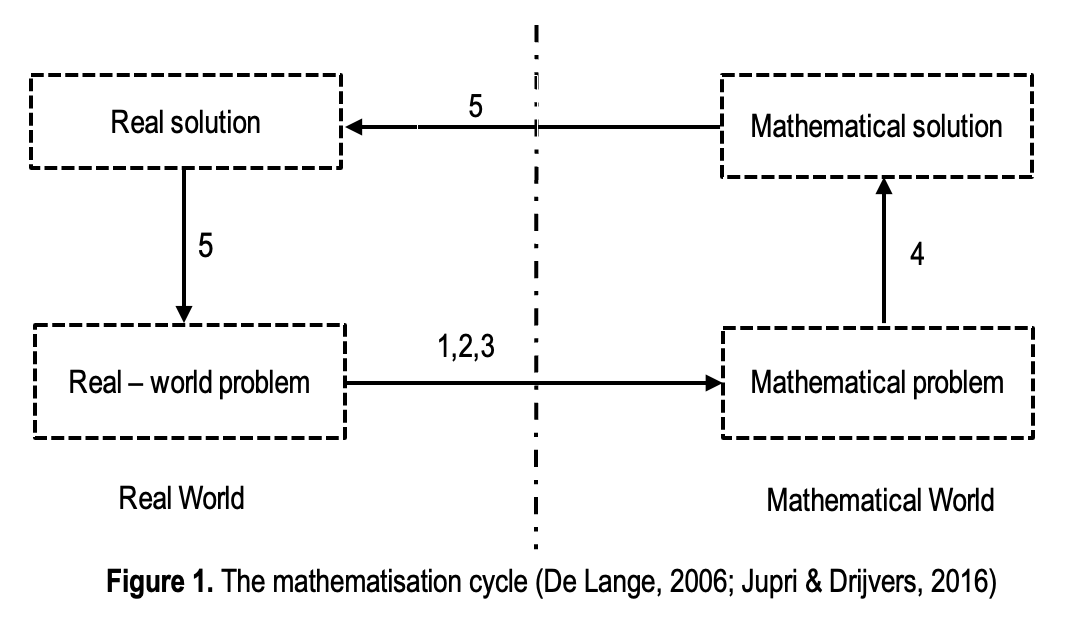
Realistic Mathematics Education (RME) has gained significant attention in Vietnam over the past decade due to its potential for enhancing mathematics instruction. This study investigates the process of mathematicization undertaken by students as they transition from solving a real-world contextual problem to discovering and applying the Law of Sines. The primary problem involves determining the angle formed by the crossbar and the hanging rope of a disco ball. Guided by the principles of RME, the mathematicization process encourages students to model this scenario as a triangle with two given side lengths and a specified angle between one side and the base. With teacher facilitation, students construct a general mathematical model and subsequently reinvent the Law of Sines. They apply this law to solve the initial problem and further extend their understanding by tackling a similar contextual scenario. The study involved 40 students, who engaged with worksheets designed to present relevant problems. Their problem-solving processes were documented and analyzed using qualitative methods. The findings contribute to the development of a teaching approach for introducing the Law of Sines within the framework of RME, specifically tailored to the Vietnamese educational context. This approach underscores the progression of students' understanding through the integration of contextual problem-solving and theoretical reinvention.
Keywords
Article Details

This work is licensed under a Creative Commons Attribution 4.0 International License.
References
- Blum, W., & Niss, M. (1991). Applied mathematical problem solving, modelling, applications, and links to other subjects - State, trends and issues in mathematics instruction. Educational Studies in Mathematics, 22(1), 37–68. https://doi.org/10.1007/BF00302716
- Boaler, J. (1993). Encouraging the transfer of ‘school’’ mathematics to the “real world” through the integration of process and content, context and culture.’ Educational Studies in Mathematics, 25(4), 341–373. https://doi.org/10.1007/BF01273906
- Da, N. T. (2022). Designing a teaching model based on the Realistic Mathematics Education (RME) approach and its application in teaching calculus. Journal of Mathematics and Science Teacher, 2(1), em006. https://doi.org/10.29333/mathsciteacher/11918
- Danh Nam, N. (2020). Some problems in realistic mathematics education. Vietnam Journal of Education, 487(1), 15–21. https://mysite.tnu.edu.vn/files/users/nguyendanhnam/487_Nguyn_Danh_Nam.pdf
- De Lange, J. (2006). Mathematical literacy for living from OECD-PISA perspective. Tsukuba Journal of Educational Study in Mathematics. Special Issue on The APEC- TSUKUBA International Conference “Innovative Teaching Mathematics through Lesson Study,” 25, 13–35. http://www.criced.tsukuba.ac.jp/math/apec2006/
- Felton, M. D. (2010). News & amp; Views: Is math politically neutral? Teaching Children Mathematics, 17(2), 60–63. https://doi.org/10.5951/TCM.17.2.0060
- Freudenthal, H. (1968). Why to teach mathematics so as to be useful. Educational Studies in Mathematics, 1(1–2), 3–8. https://doi.org/10.1007/BF00426224
- Freudenthal, H. (1971). Geometry between the devil and the deep sea. Educational Studies in Mathematics, 3(3–4), 413–435. https://doi.org/10.1007/BF00302305
- Freudenthal, H. (1983). Didactical Phenomenology of Mathematical Structures. Reidel Publishing Company.
- Freudenthal, H. (2002). Revisiting Mathematics Education: China lectures (Vol. 9). Kluwer Academic Publishers. https://doi.org/10.1007/0-306-47202-3
- Gravemeijer, K. (1994a). Developing realistic mathematics education. CD β Press. https://www.fisme.science.uu.nl/publicaties/literatuur/1994_gravemeijer_dissertation_0_222.pdf
- Gravemeijer, K. (1994b). Modelling two-digit addition and subtraction with an empty number line. In: T. Breiteig, G. Kaiser-Messmer and I. Huntley. Mathematics works – Mathematical Modelling in the Classroom. Ellis Horwood / Simon and Schuster.
- Gravemeijer, K. (1999). How Emergent Models May Foster the Constitution of Formal Mathematics. Mathematical Thinking and Learning, 1(2), 155–177. https://doi.org/10.1207/s15327833mtl0102_4
- Gravemeijer, K., & Doorman, M. (1999). Context Problems in Realistic Mathematics Education: A Calculus Course as an Example. Educational Studies in Mathematics, 39(1/3), 111–129. https://doi.org/10.1023/A:1003749919816
- Gravemeijer, K., & Terwel, J. (2000). Hans Freudenthal: A mathematician on didactics and curriculum theory. Journal of Curriculum Studies, 32(6), 777–796. https://doi.org/10.1080/00220270050167170
- Hendroanto, A., van Galen, F., Van Eerde, D., Prahmana, R. C. I., Setyawan, F., & Istiandaru, A. (2018). Photography activities for developing students’ spatial orientation and spatial visualization. Journal of Physics: Conference Series, 943(1), 012029. http://dx.doi.org/10.1088/1742-6596/943/1/012029
- Inci, A. M., Peker, B., & Kucukgencay, N. (2023). Realistic mathematics education. In book: Current Studies in Educational Disciplines 2023 (pp.66-83) Edition 1, Chapter 5. Publisher: ISRES Publishing. ISRES Publishing. https://www.researchgate.net/publication/377209600_Realistic_Mathematics_Education
- Johnson, P., Almuna, F., & Silva, M. (2022). The role of problem context familiarity in modelling first-order ordinary differential equations. Journal on Mathematics Education, 13(2), 323–336. https://doi.org/10.22342/jme.v13i2.pp323-336
- Jupri, A., & Drijvers, P. (2016). Student Difficulties in Mathematizing Word Problems in Algebra. EURASIA Journal of Mathematics, Science and Technology Education, 12(9), 2481–2502. https://doi.org/10.12973/eurasia.2016.1299a
- Kant, D., & Sarikaya, D. (2021). Mathematizing as a virtuous practice: different narratives and their consequences for mathematics education and society. Synthese, 199(1–2), 3405–3429. https://doi.org/10.1007/s11229-020-02939-y
- Larsen, S. (2018). Didactical phenomenology: the engine that drives realistic mathematics education. For the Learning of Mathematics, 38(3), 25–29. https://www.jstor.org/stable/26548508
- Le, T. T., Pham, A. G., & Nguyen, T. T. (2021). Applying realistic mathematics education theory in teaching: some challenges, principles and recommendations. Vietnam Journal of Education, 494(2), 37–43. https://tcgd.tapchigiaoduc.edu.vn/index.php/tapchi/article/view/22
- Loc, N. P., Tran, N., & Tien, T. (2020). Approach To Realistic Mathematics Education In Teaching Mathematics: A Case Of Cosine Theorem-Geometry 10. International Journal of Scientific & Technology Research, 8, 1173–1178. www.ijstr.org
- Nguyen, T. T., Trinh, T. P. T., Ngo, H. T. V., Hoang, N. A., Tran, T., Pham, H. H., & Bui, V. N. (2020). Realistic mathematics education in Vietnam: Recent policies and practices. International Journal of Education and Practice, 8(1), 57–71. https://doi.org/10.18488/journal.61.2020.81.57.71
- Nkambule, T. (2009). Teaching and learning linear programming in a grade 11 multilingual mathematics class of English language learners: exploring the deliberate use of learners’ home language. In Pytagoras (Vol. 71). https://wiredspace.wits.ac.za/server/api/core/bitstreams/2fa4b36b-2db3-4630-b535-41700db0041e/content
- Pierce, R. U., & Stacey, K. C. (2006). Enhancing the image of mathematics by association with simple pleasures from real world contexts. ZDM, 38(3), 214–225. https://doi.org/10.1007/BF02652806
- Rasmussen, C., Zandieh, M., King, K., & Teppo, A. (2005). Advancing Mathematical Activity: A Practice-Oriented View of Advanced Mathematical Thinking. Mathematical Thinking and Learning, 7(1), 51–73. https://doi.org/10.1207/s15327833mtl0701_4
- Risdiyanti, I., & Prahmana, R. C. I. (2020). The learning trajectory of number pattern learning using "Barathayudha" war stories and uno stacko. Journal on Mathematics Education, 11(1), 157-166. http://doi.org/10.22342/jme.11.1.10225.157-166
- Streefland, L. (1985). Wiskunde als activiteit en de realiteit als bron (Mathematics as an activity and reality as a source). Nieuwe Wiskrant, 5(1), 60–67. http://www.fisme.science.uu.nl/wiskrant/artikelen/artikelen00-10/051/0501september_streefland.pdf
- Streefland, L. (1991). Fraction in Realistic Mathematics Education, A paradigm of developmental research. Kluwer Academic Publisher.
- Treffers, A. (1987). Three dimensions. A model of goal and theory description in mathematics instruction: The Wiskobas Project. Springer Dordrecht.
- Treffers, A. (1991). Didactical background of a mathematics program for primary education. In: L. Streefland (ed.). Realistic mathematics education in primary school. In Realistic mathematics education in primary school (pp. 21–56). CDß press/Freudenthal Institute, Utrecht University, Utrecht, The Netherlands. https://www.fisme.science.uu.nl/publicaties/literatuur/1991_streefland_0-209.pdf
- Van Den Heuvel-Panhuizen, M. (2000). Mathematics education in the Netherlands: A guided tour 1. Freudenthal Institute CD-rom for International Commission on Mathematics Education (ICME) 9. https://p4mriunismuh.wordpress.com/wp-content/uploads/2010/08/mathematics-education-in-the-netherlands.pdf
- Van Den Heuvel-Panhuizen, M. (2003). The didactical use of models in realistic mathematics education: An example from a longitudinal trajectory on percentage. Educational Studies in Mathematics, 54(1), 9–35. https://doi.org/10.1023/B:EDUC.0000005212.03219.dc
- Van Den Heuvel-Panhuizen, M. (2005). The role of contexts in assessment problems in mathematics. For the Learning of Mathematics, 25(2), 2–23.
- Van den Heuvel-Panhuizen, M., & Drijvers, P. (2014). Realistic Mathematics Education. In Encyclopedia of Mathematics Education (pp. 521–525). Springer Netherlands. https://doi.org/10.1007/978-94-007-4978-8_170
- Van den Heuvel-Panhuizen, M., & Drijvers, P. (2020). Realistic Mathematics Education. In Encyclopedia of Mathematics Education (pp. 713–717). Springer International Publishing. https://doi.org/10.1007/978-3-030-15789-0_170
- Van den Heuvel-Panhuizen, M., & Wijers, M. (2005). Mathematics standards and curricula in the Netherlands. Zentralblatt Für Didaktik Der Mathematik, 37(4), 287–307. https://doi.org/10.1007/BF02655816
- Vietnam Mathematics General Education Curriculum, Pub. L. No. 32/2018/TT-BGDĐT (2018).
- Yackel, E., Stephan, M., Rasmussen, C., & Underwood, D. (2003). Didactising: Continuing the work of Leen Streefland. Educational Studies in Mathematics, 54(1), 101–126. https://doi.org/10.1023/B:EDUC.0000005213.85018.34
References
Blum, W., & Niss, M. (1991). Applied mathematical problem solving, modelling, applications, and links to other subjects - State, trends and issues in mathematics instruction. Educational Studies in Mathematics, 22(1), 37–68. https://doi.org/10.1007/BF00302716
Boaler, J. (1993). Encouraging the transfer of ‘school’’ mathematics to the “real world” through the integration of process and content, context and culture.’ Educational Studies in Mathematics, 25(4), 341–373. https://doi.org/10.1007/BF01273906
Da, N. T. (2022). Designing a teaching model based on the Realistic Mathematics Education (RME) approach and its application in teaching calculus. Journal of Mathematics and Science Teacher, 2(1), em006. https://doi.org/10.29333/mathsciteacher/11918
Danh Nam, N. (2020). Some problems in realistic mathematics education. Vietnam Journal of Education, 487(1), 15–21. https://mysite.tnu.edu.vn/files/users/nguyendanhnam/487_Nguyn_Danh_Nam.pdf
De Lange, J. (2006). Mathematical literacy for living from OECD-PISA perspective. Tsukuba Journal of Educational Study in Mathematics. Special Issue on The APEC- TSUKUBA International Conference “Innovative Teaching Mathematics through Lesson Study,” 25, 13–35. http://www.criced.tsukuba.ac.jp/math/apec2006/
Felton, M. D. (2010). News & amp; Views: Is math politically neutral? Teaching Children Mathematics, 17(2), 60–63. https://doi.org/10.5951/TCM.17.2.0060
Freudenthal, H. (1968). Why to teach mathematics so as to be useful. Educational Studies in Mathematics, 1(1–2), 3–8. https://doi.org/10.1007/BF00426224
Freudenthal, H. (1971). Geometry between the devil and the deep sea. Educational Studies in Mathematics, 3(3–4), 413–435. https://doi.org/10.1007/BF00302305
Freudenthal, H. (1983). Didactical Phenomenology of Mathematical Structures. Reidel Publishing Company.
Freudenthal, H. (2002). Revisiting Mathematics Education: China lectures (Vol. 9). Kluwer Academic Publishers. https://doi.org/10.1007/0-306-47202-3
Gravemeijer, K. (1994a). Developing realistic mathematics education. CD β Press. https://www.fisme.science.uu.nl/publicaties/literatuur/1994_gravemeijer_dissertation_0_222.pdf
Gravemeijer, K. (1994b). Modelling two-digit addition and subtraction with an empty number line. In: T. Breiteig, G. Kaiser-Messmer and I. Huntley. Mathematics works – Mathematical Modelling in the Classroom. Ellis Horwood / Simon and Schuster.
Gravemeijer, K. (1999). How Emergent Models May Foster the Constitution of Formal Mathematics. Mathematical Thinking and Learning, 1(2), 155–177. https://doi.org/10.1207/s15327833mtl0102_4
Gravemeijer, K., & Doorman, M. (1999). Context Problems in Realistic Mathematics Education: A Calculus Course as an Example. Educational Studies in Mathematics, 39(1/3), 111–129. https://doi.org/10.1023/A:1003749919816
Gravemeijer, K., & Terwel, J. (2000). Hans Freudenthal: A mathematician on didactics and curriculum theory. Journal of Curriculum Studies, 32(6), 777–796. https://doi.org/10.1080/00220270050167170
Hendroanto, A., van Galen, F., Van Eerde, D., Prahmana, R. C. I., Setyawan, F., & Istiandaru, A. (2018). Photography activities for developing students’ spatial orientation and spatial visualization. Journal of Physics: Conference Series, 943(1), 012029. http://dx.doi.org/10.1088/1742-6596/943/1/012029
Inci, A. M., Peker, B., & Kucukgencay, N. (2023). Realistic mathematics education. In book: Current Studies in Educational Disciplines 2023 (pp.66-83) Edition 1, Chapter 5. Publisher: ISRES Publishing. ISRES Publishing. https://www.researchgate.net/publication/377209600_Realistic_Mathematics_Education
Johnson, P., Almuna, F., & Silva, M. (2022). The role of problem context familiarity in modelling first-order ordinary differential equations. Journal on Mathematics Education, 13(2), 323–336. https://doi.org/10.22342/jme.v13i2.pp323-336
Jupri, A., & Drijvers, P. (2016). Student Difficulties in Mathematizing Word Problems in Algebra. EURASIA Journal of Mathematics, Science and Technology Education, 12(9), 2481–2502. https://doi.org/10.12973/eurasia.2016.1299a
Kant, D., & Sarikaya, D. (2021). Mathematizing as a virtuous practice: different narratives and their consequences for mathematics education and society. Synthese, 199(1–2), 3405–3429. https://doi.org/10.1007/s11229-020-02939-y
Larsen, S. (2018). Didactical phenomenology: the engine that drives realistic mathematics education. For the Learning of Mathematics, 38(3), 25–29. https://www.jstor.org/stable/26548508
Le, T. T., Pham, A. G., & Nguyen, T. T. (2021). Applying realistic mathematics education theory in teaching: some challenges, principles and recommendations. Vietnam Journal of Education, 494(2), 37–43. https://tcgd.tapchigiaoduc.edu.vn/index.php/tapchi/article/view/22
Loc, N. P., Tran, N., & Tien, T. (2020). Approach To Realistic Mathematics Education In Teaching Mathematics: A Case Of Cosine Theorem-Geometry 10. International Journal of Scientific & Technology Research, 8, 1173–1178. www.ijstr.org
Nguyen, T. T., Trinh, T. P. T., Ngo, H. T. V., Hoang, N. A., Tran, T., Pham, H. H., & Bui, V. N. (2020). Realistic mathematics education in Vietnam: Recent policies and practices. International Journal of Education and Practice, 8(1), 57–71. https://doi.org/10.18488/journal.61.2020.81.57.71
Nkambule, T. (2009). Teaching and learning linear programming in a grade 11 multilingual mathematics class of English language learners: exploring the deliberate use of learners’ home language. In Pytagoras (Vol. 71). https://wiredspace.wits.ac.za/server/api/core/bitstreams/2fa4b36b-2db3-4630-b535-41700db0041e/content
Pierce, R. U., & Stacey, K. C. (2006). Enhancing the image of mathematics by association with simple pleasures from real world contexts. ZDM, 38(3), 214–225. https://doi.org/10.1007/BF02652806
Rasmussen, C., Zandieh, M., King, K., & Teppo, A. (2005). Advancing Mathematical Activity: A Practice-Oriented View of Advanced Mathematical Thinking. Mathematical Thinking and Learning, 7(1), 51–73. https://doi.org/10.1207/s15327833mtl0701_4
Risdiyanti, I., & Prahmana, R. C. I. (2020). The learning trajectory of number pattern learning using "Barathayudha" war stories and uno stacko. Journal on Mathematics Education, 11(1), 157-166. http://doi.org/10.22342/jme.11.1.10225.157-166
Streefland, L. (1985). Wiskunde als activiteit en de realiteit als bron (Mathematics as an activity and reality as a source). Nieuwe Wiskrant, 5(1), 60–67. http://www.fisme.science.uu.nl/wiskrant/artikelen/artikelen00-10/051/0501september_streefland.pdf
Streefland, L. (1991). Fraction in Realistic Mathematics Education, A paradigm of developmental research. Kluwer Academic Publisher.
Treffers, A. (1987). Three dimensions. A model of goal and theory description in mathematics instruction: The Wiskobas Project. Springer Dordrecht.
Treffers, A. (1991). Didactical background of a mathematics program for primary education. In: L. Streefland (ed.). Realistic mathematics education in primary school. In Realistic mathematics education in primary school (pp. 21–56). CDß press/Freudenthal Institute, Utrecht University, Utrecht, The Netherlands. https://www.fisme.science.uu.nl/publicaties/literatuur/1991_streefland_0-209.pdf
Van Den Heuvel-Panhuizen, M. (2000). Mathematics education in the Netherlands: A guided tour 1. Freudenthal Institute CD-rom for International Commission on Mathematics Education (ICME) 9. https://p4mriunismuh.wordpress.com/wp-content/uploads/2010/08/mathematics-education-in-the-netherlands.pdf
Van Den Heuvel-Panhuizen, M. (2003). The didactical use of models in realistic mathematics education: An example from a longitudinal trajectory on percentage. Educational Studies in Mathematics, 54(1), 9–35. https://doi.org/10.1023/B:EDUC.0000005212.03219.dc
Van Den Heuvel-Panhuizen, M. (2005). The role of contexts in assessment problems in mathematics. For the Learning of Mathematics, 25(2), 2–23.
Van den Heuvel-Panhuizen, M., & Drijvers, P. (2014). Realistic Mathematics Education. In Encyclopedia of Mathematics Education (pp. 521–525). Springer Netherlands. https://doi.org/10.1007/978-94-007-4978-8_170
Van den Heuvel-Panhuizen, M., & Drijvers, P. (2020). Realistic Mathematics Education. In Encyclopedia of Mathematics Education (pp. 713–717). Springer International Publishing. https://doi.org/10.1007/978-3-030-15789-0_170
Van den Heuvel-Panhuizen, M., & Wijers, M. (2005). Mathematics standards and curricula in the Netherlands. Zentralblatt Für Didaktik Der Mathematik, 37(4), 287–307. https://doi.org/10.1007/BF02655816
Vietnam Mathematics General Education Curriculum, Pub. L. No. 32/2018/TT-BGDĐT (2018).
Yackel, E., Stephan, M., Rasmussen, C., & Underwood, D. (2003). Didactising: Continuing the work of Leen Streefland. Educational Studies in Mathematics, 54(1), 101–126. https://doi.org/10.1023/B:EDUC.0000005213.85018.34