Article Sidebar

Download
PDF
Statistic
Read Counter : 4 Download : 0

Downloads

Download data is not yet available.

Main Article Content

Abstract

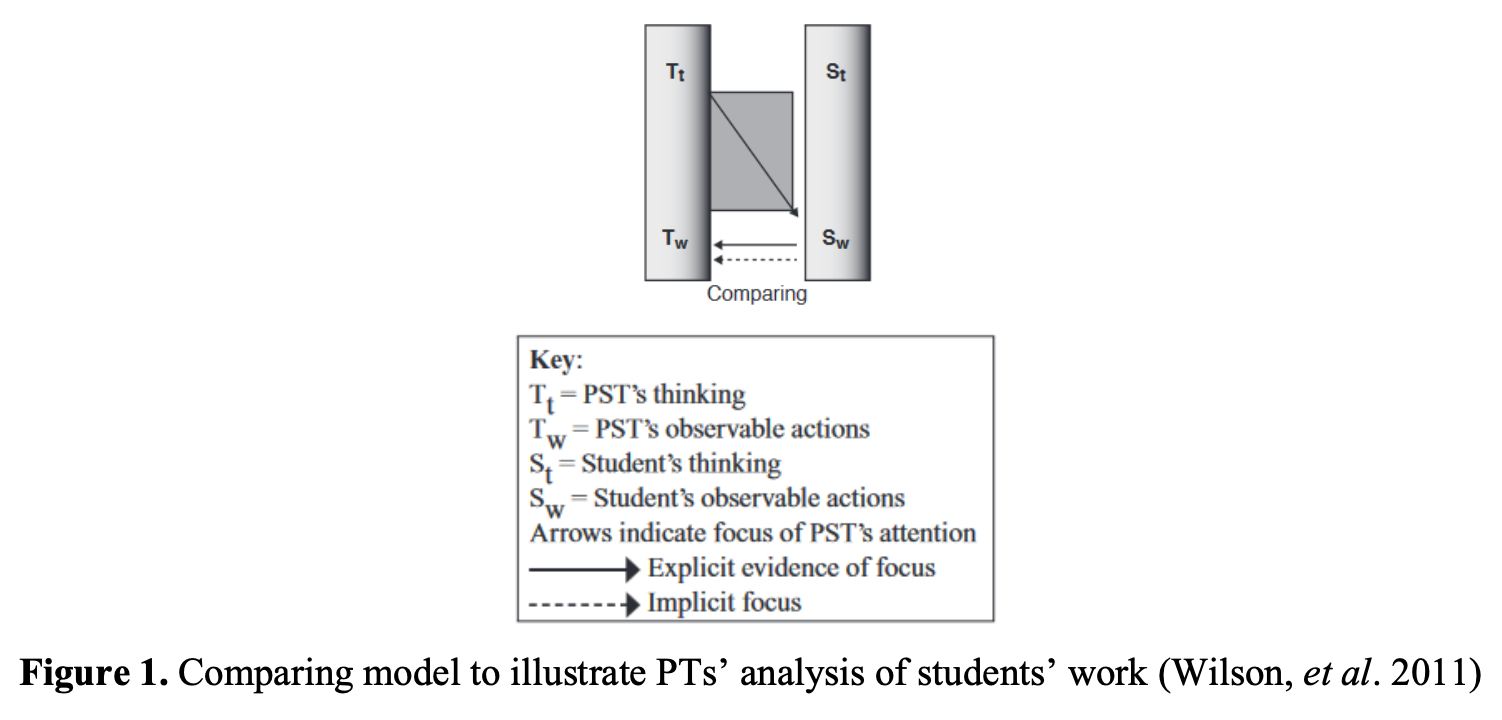
Mathematical thinking is an important aspect of mathematics education and, therefore, also needs to be understood by prospective teachers. Prospective teachers should have the ability to analyze and interpret students’ mathematical thinking. Comparing model is one of the interpretation models from Wilson, Lee, and Hollebrands. This article will describe the prospective teacher used the model of the building process in interpretation students' mathematical thinking. Subjects selected by considering them in following the students’ strategies in solving the Building Construction Problem. Comparing model is a model of interpretation in which a person interprets student thinking based on student work. There are two types comparing model building process prospective teacher use in interpreting students’ mathematical thinking ie. comparing work and comparing knowledge. In comparing works, prospective teachers use an external representation rubric. This is used to analyze student activities in order to provide an interpretation that is comparing the work of students with their own work. In comparing knowledge, prospective teachers use internal representation rubrics to provide interpretation by comparing the students' work with their knowledge or thought.

Keywords

Comparing Model Interpretation Students’ Mathematical Thinking

Article Details

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite
Sapti, M., Purwanto, Irawan, E. B., As’ari, A. R., Sa’dijah, C., Susiswo, & Wijaya, A. (2019). Comparing model-building process: A model prospective teachers used in interpreting students’ mathematical thinking. Journal on Mathematics Education, 10(2), 171–184. Retrieved from https://jme.ejournal.unsri.ac.id/index.php/jme/article/view/3786
Download Citation
Endnote/Zotero/Mendeley (RIS)
BibTeX

References

  1. Ahmad, S., Prahmana, R.C.I., Kenedi, A.K., Helsa, Y., Arianil, Y., & Zainil, M. (2018). The instruments of higher order thinking skills. Journal of Physics: Conference Series, 943(1), 012053. http://doi.org/ 10.1088/1742-6596/943/1/012053.
  2. Brookhart, S.M. (2013). How to create and use rubrics for formative assessment and grading.
  3. Alexandria, VA: ASCD.
  4. Cobb, P., & Steffe, L.P. (1983). The constructivist researcher as teacher and model builder. Journal for Research in Mathematics Education, 14(2), 83–94. https://doi.org/10.1007/978-90-481- 9729-3_3.
  5. Cuoco, A.A. (2001). The Role of Representation in School Mathematics 2001 Yearbook. Reston, VA: National Council of Teachers of Mathematics.
  6. Fernández, C., Llinares, S., & Valls, J. (2012). Learning to notice students’ mathematical thinking through on-line discussions. ZDM - International Journal on Mathematics Education, 44(6), 747–759. http://doi.org/10.1007/s11858-012-0425-y.
  7. Hendroanto, A., van Galen, F., van Eerde, D., Prahmana, R.C.I., Setyawan, F., & Istiandaru, A. (2018). Photography activities for developing students’ spatial orientation and spatial visualization. Journal of Physics: Conference Series, 943(1), 012029. http://doi.org/10.1088/1742-6596/943/1/012029.
  8. Jacobs, V.R., Lamb, L.L.C., & Philipp, R.A. (2010). Professional noticing of children’s mathematical thinking. Journal for Research in Mathematics Education Journal for Research in Mathematics Education, 41(2), 169–202. http://doi.org/10.2307/20720130.
  9. Janvier, C., Girardon, C., & Morand, J. (1993). Mathematical symbols and representations. In P. S. Wilson (Ed.), Research Ideas for the Classroom: High School Mathematics (p. 81). Reston, VA: NCTM.
  10. Mason, J. (2011). Noticing roots and branches. In M.G. Sherin, V.J. Jacobs, & R. Phillip (Eds.), Mathematics Teacher Noticing Seeing Through Teachers’ Eyes (pp. 35–50). New York: Routledge. http://doi.org/10.4324/9780203832714.
  11. Murtafiah, W., Sa’dijah, C., Candra, T.D., & As’ari, A.R. (2018). Exploring The Explanation of Pre- service Teacher in Mathematics Teaching Practice. Journal on Mathematics Education, 9(2), 259–270.
  12. Norton, A., McCloskey, A., & Hudson, R.A. (2011). Prediction assessments: Using video-based predictions to assess prospective teachers’ knowledge of students’ mathematical thinking. Journal of Mathematics Teacher Education, 14(4), 305–325. http://doi.org/10.1007/s10857- 011-9181-0.
  13. Polya, G. (1945). How To Solve It. New Jersey: Princeton University Press.
  14. Sapti, M., Purwanto, Mulyati, S., & Irawan, E.B. (2016). Pre-service teacher interpretations of students’ mathematical understanding. In Proceeding of 3rd International Conference on
  15. Research, Implementation and Education of Mathematics and Science (pp. 435–442). Yogyakarta: Faculty of Mathematics and Natural Science Yogyakarta State University.
  16. Shahrill, M., Putri, R.I.I., Zulkardi, & Prahmana, R.C.I. (2018). Processes involved in solving mathematical problems. AIP Conference Proceedings, 1952(1), 020019. https://doi.org/10.1063/1.5031981.
  17. Sherin, M.G., Jacobs, V.R., & Philipp, R.A. (2011). Mathematics Teacher Noticing Seeing through Teachers’ Eyes. New York: Roudledge-Falmer. http://doi.org/10.4324/9780203832714.
  18. Simon, M.A., & Tzur, R. (1999). Explicating the teacher’s perspective from the researchers’ perspectives: Generating accounts of mathematics teachers’ practice. Journal for Research in Mathematics Education, 30(4), 252–264. http://doi.org/10.2307/749835.
  19. Sleep, L., & Boerst, T.A. (2012). Preparing beginning teachers to elicit and interpret students’ mathematical thinking. Teaching and Teacher Education, 28(7), 1038–1048. http://doi.org/10.1016/j.tate.2012.04.005.
  20. Stacey, K. (2006). What is mathematical thinking and why is it important. Progress report of the APEC project: collaborative studies on innovations for teaching and learning mathematics in different cultures (II)—Lesson study focusing on mathematical thinking.
  21. Steffe, L.P., & Thompson, P.W. (2000). Teaching experiment methodology: Underlying principles and essential elements. In R. Lesh & A. E. Kelly (Eds.), Research Design in Mathematics and Science Education (pp. 267–307). Hillsdale, NJ: Erlbaum.
  22. Swartz, R. (2012). Infusing instruction in thinking into content instruction: What do we know about its success? Sri Lanka Journal of Educational Research, 1–39.
  23. van Es, E. A., & Sherin, M.G. (2002). Learning to notice: Scaffolding new teachers’ interpretations of classroom interactions. Journal of Technology and Teacher Education, 10(4), 571–596.
  24. Widodo, S.A., Istiqomah, Leonard, Nayazik, A., & Prahmana, R.C.I. (2019). Formal student thinking in mathematical problem-solving. Journal of Physics: Conference Series, 1188(1), 012087. http://doi.org/10.1088/1742-6596/1188/1/012087.
  25. Wilson, P.H., Lee, H.S., & Hollebrands, K.F. (2011). Understanding prospective mathematics teachers’ processes for making sense of students’ work with technology. Journal for Research in Mathematics Education, 42(1), 39–64. http://doi.org/10.5951/jresematheduc.42.1.0039.
  26. Zhu, Y., Yu, W., & Cai, J. (2018). Understanding students’ mathematical thinking for effective teaching: A comparison between expert and nonexpert Chinese elementary mathematics teachers. Eurasia Journal of Mathematics, Science and Technology Education, 14(1), 213–224. http://doi.org/10.12973/ejmste/78241.

Most read articles by the same author(s)

1 2 > >>